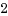Rev.1を表示中。最新版はこちら。

red black treeはノードを赤/黒とし、以下の条件のバイナリツリーです。パスの階層が、平均的になり、平均した負荷で各オブジェクトを検索できるようになっています。カーネルでは仮想メモリオブジェクト(struct vm_area_struct)でアドレスを大小として管理するのに使われています。

・トップは黒ノード
・赤の子は黒(黒の制約はありません。)
・トップからのパスの黒数は同じ

まず新規ノードを追加するシンプルなケースです。追加ノードは赤となり、処理が必要なのは追加位置が赤の場合で、黒だと追加して終了となります。

親ノードと叔父ノードを黒に、そして祖父ノードを赤にします。(親が赤なら祖父は黒でなければなりません。)そうすることで各パスの黒数の変化はありません。（実装では、祖父を赤として新規追加する。とし同じ処理が順次上に遡って繰り返されます。）


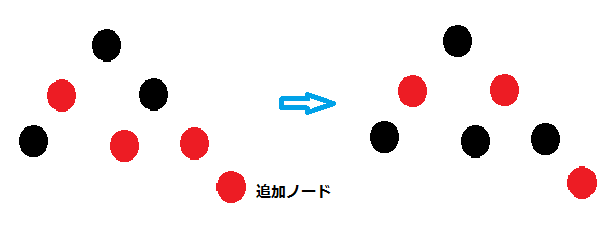
特異なケースとしては、叔父ノードが黒の場合です。親を赤から黒に変えますが、叔父ノードを黒に変えることはできません。で、叔父ノードのパスの黒数が１つなくなります。そこで登場するのが回転です。


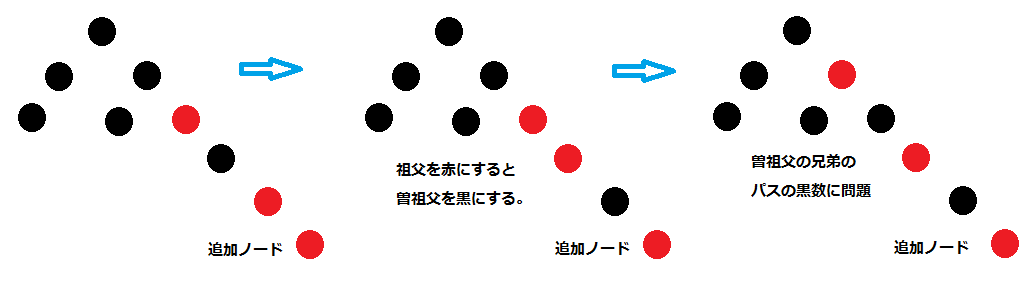
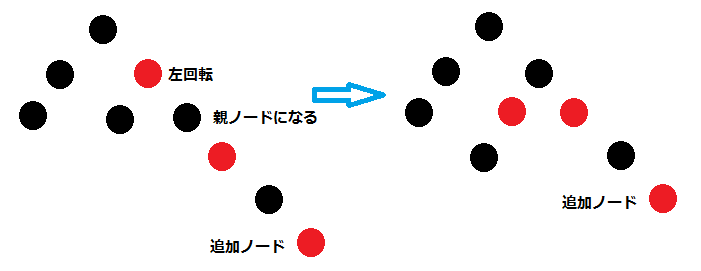
回転とは親と子を差し替えることで、左回転とは、親ノードを子ノードの左ノードとすることです。子の左ノード接続するには、親より大きい子ノードとなり、従って右子ノードとの差し替えです。左回転の目的は、１つ多い右パスの黒ノードを両パス共通ノードとすることで、１つ多かった黒数が解消されます。上の説明のように、これは赤黒の子ノードを持つ親ノードで、赤の子ノードが黒になり黒の親ノードが赤になるケースです。上記内容を踏まえ実装をみてもらえれば、理解できるかと思います。


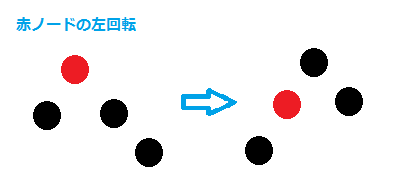
特異なケースで回転をすることで赤黒木が作成できます


以下カーネルでの実装です。__vma_link_rb()は仮想メモリstruct mm_struct *mm, structを、赤黒木にノードを登録します。mm->mm_rbはルートで、vma->vm_rbが登録するノードです。ノードの大小はmm->addrで赤黒木から取得します。

rb_link_node()でノードを設定し、rb_insert_color()で赤黒木の条件に添って登録します。

static void __vma_link_rb(struct mm_struct *mm, struct vm_area_struct *vma,
                       struct rb_node **rb_link, struct rb_node *rb_parent)
{
       rb_link_node(&vma->vm_rb, rb_parent, rb_link);
       rb_insert_color(&vma->vm_rb, &mm->mm_rb);
}

rb_link_node()でノードを赤とします。従って新規登録するノードは赤となり、ここでは親の色は考慮しません。

static inline void rb_link_node(struct rb_node * node, struct rb_node * parent,
                               struct rb_node ** rb_link)
{
       node->rb_parent = parent;
       node->rb_color = RB_RED;
       node->rb_left = node->rb_right = NULL;

       *rb_link = node;
}

左回転で、nodeと右子ノードと差し替えます。node右に、右子ノードの左子ノードを接続し、左子ノードの親をnodeとし(ただし右子ノードがある場合)、右子ノードに左にnodeを接続します。

右子ノードの親をnodeの親にします。もしnodeの親がなけらばnodeはルートです。rootを右子ノードに差し替えます。

rootでない場合、node自身が右子ノードなら、その親の右側に右子ノードを、そうでないなら左に右子ノードを接続します。

最後にnodeの親を、右子ノードして完了です。

static void __rb_rotate_left(struct rb_node *node, struct rb_root *root)
{
       struct rb_node *right = node->rb_right;

       if ((node->rb_right = right->rb_left))　　　　
               right->rb_left->rb_parent = node;
       right->rb_left = node;

       if ((right->rb_parent = node->rb_parent))
       {
               if (node == node->rb_parent->rb_left)
                       node->rb_parent->rb_left = right;
               else
                       node->rb_parent->rb_right = right;
       }
       else
               root->rb_node = right;
       node->rb_parent = right;
}

右回転でnodeと左子ノードと差し替えます。

static void __rb_rotate_right(struct rb_node *node, struct rb_root *root)
{
       struct rb_node *left = node->rb_left;

       if ((node->rb_left = left->rb_right))
               left->rb_right->rb_parent = node;
       left->rb_right = node;

       if ((left->rb_parent = node->rb_parent))
       {
               if (node == node->rb_parent->rb_right)
                       node->rb_parent->rb_right = left;
               else
                       node->rb_parent->rb_left = left;
       }
       else
               root->rb_node = left;
       node->rb_parent = left;
}

rb_insert_color()で赤黒木の本質です。insertと挿入のイメージですが、実際は挿入はrb_link_node()で完了しています。ここではノードの親が赤か黒かの正当性のチェックをし、必要に応じて赤黒を変更していきます。

考え方は、上の内の通りで、親/叔父/祖父の色変更を、対象ノードから順にrootとなるか接続ノードが黒となるまで遡っていくことです。兄弟が赤/黒でそれが右/左かによって回転方向が異なり、そのチェックが必要で、頭の体操のような実装となります。

void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
       struct rb_node *parent, *gparent;

       while ((parent = node->rb_parent) && parent->rb_color == RB_RED)
       {
               gparent = parent->rb_parent;
               if (parent == gparent->rb_left)
               {
                       {
                               register struct rb_node *uncle = gparent->rb_right;
                               if (uncle && uncle->rb_color == RB_RED)
                               {
                                       uncle->rb_color = RB_BLACK;
                                       parent->rb_color = RB_BLACK;
                                       gparent->rb_color = RB_RED;
                                       node = gparent;
                                       continue;
                               }
                       }

                       if (parent->rb_right == node)
                       {
                               register struct rb_node *tmp;
                               __rb_rotate_left(parent, root);
                               tmp = parent;
                               parent = node;
                               node = tmp;
                       }

                       parent->rb_color = RB_BLACK;
                       gparent->rb_color = RB_RED;
                       __rb_rotate_right(gparent, root);
               } else {
                       {
                               register struct rb_node *uncle = gparent->rb_left;
                               if (uncle && uncle->rb_color == RB_RED)
                               {
                                       uncle->rb_color = RB_BLACK;
                                       parent->rb_color = RB_BLACK;
                                       gparent->rb_color = RB_RED;
                                       node = gparent;
                                       continue;
                               }
                       }

                       if (parent->rb_left == node)
                       {
                               register struct rb_node *tmp;
                               __rb_rotate_right(parent, root);
                               tmp = parent;
                               parent = node;
                               node = tmp;
                       }

                       parent->rb_color = RB_BLACK;
                       gparent->rb_color = RB_RED;
                       __rb_rotate_left(gparent, root);
               }
       }

       root->rb_node->rb_color = RB_BLACK;
}

追記

赤黒木とはこのような物と言う事で、linuxの機能的な物とは関係ありませんが、頭の体操にはもってこいです。